높이맵편집에 있어서 코사인 함수를 이용한 부드러운 지형편집 기법
프로그래밍/3D프로그래밍 2006/07/21 18:43 코사인 함수를 이용한 부드러운 지형편집 기법 by Xevious7
http://www.xevious7.com/107 2006.7.21 , 최종수정 2006.8.7.
들어가는 글
3D지형에서 보통 Rawmap 이라고 불리는 높이맵 즉 높이값만 가지는
데이타를 가지고 지형을 형성할때 부드러운 모양의 지형을 만들기
위해 가장 많이 쓰여지고 있는 기법은 가우시안 함수를 이용한 기법인 것 같습니다.
확률.통계에서는 가우시안함수는 정규분포로도 잘 알려져 있으며
아주 여러분야에서 이용하고 있는 수학함수 입니다.
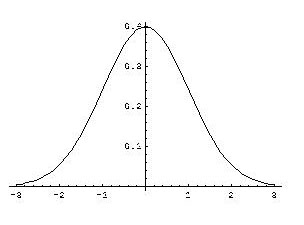 [그림] 가우시안 정규분포
[그림] 가우시안 정규분포
그런데 이 함수의 기하학적인 모양이 부드럽게 높이 솟은 산의 모양을 가지기
때문에 3D지형의 높이맵의 부드러운 지형을 위해 쓰여지는 것입니다.
물론 정밀한 손의 놀림에 의한 편집에 의해서 가능하지만 일단 어느정도
자동생성은 작업의 효율을 높이기 때문에 지형맵 툴에서 많이 사용되어지는
것 같습니다.
헌데 이 가우시안 함수는 지수함수의 공식을 가지고 있는 놈이라서
생각보다 복잡합니다. 따라서 물론 미리 계산된 셋을 가지고 적절히 조절하여
사용하는 방법을 더 많이 쓸것이고 , 아니면 소위 가우시안 필터라고 불리우는
정형화된 셋과 알고리즘을 통한 격자필터를 사용하기도 합니다. 또는 랜덤값을
통한 확률분포로 가우시안 분포를 만들어 사용하기도 합니다.
어찌 되었든 이부분에 대한 많은 문서와 구현예들이 존재하고 있습니다.
다음은 관련링크입니다.(주의: 이 링크들은 웹사이트의 사정에 의해서
깨져있을 수 있습니다.) (다른 링크를 알고 계시면 덧글을 달아주시면
감사하겠습니다. )
코사인곡선의 고찰
코사인 곡선의 모양도(사인곡선도 위상만 틀린뿐 같은 곡선이지만 계산의 편의를
위해 코사인곡선을 사용했습니다.) 완만한 산의 모양을 가지고 있습니다.
그래서 그 코사인 곡선을 이용하는 방법을 생각해보았습니다.
이 문서는 제가 생각해본 코사인 곡선을 이용한 높이맵 지형편집에 대한
문서입니다.
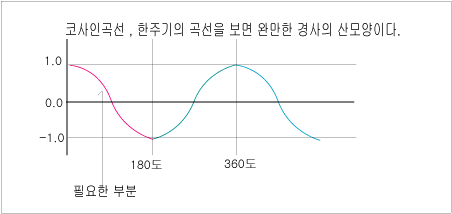
[그림] 코사인곡선
그림처럼 각도에 따른 값을 축으로 그린 코사인 곡선은 그림과 같은 모양을 가집니다.
여기서 우리가 필요한 부분은 0도에서 180도 부분입니다.
이 부분 값만 있으면 너비(즉 주기)를 조정해서 좀더 뽀죡해 보이는 곡선 또는
완만한 곡선이 가능하고 그것을 다시 미러링하고 회전하면 부드럽게 올라온
산또는 언덕 비슷한 모양을 만들수 있기 때문입니다.
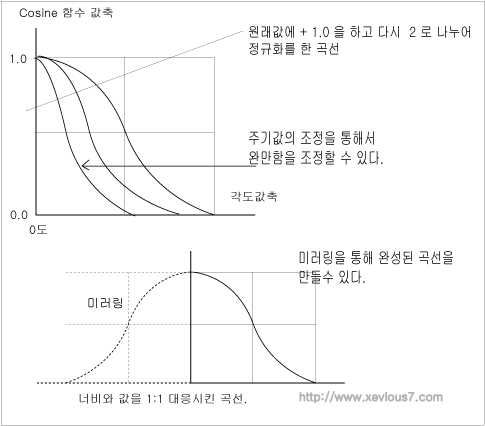
[그림] 코사인 곡선의 고찰
코사인 곡선의 높이맵적용
아날로그적으로 이해는 쉽지만 이것을 격자로 되어있는 nxn 의 높이맵의
한 정점에 이값들을 적용시켜서 그 모양을 만들려고 생각하면 격자의 크기에 따라
값들이 일정간격별로 정해져야 합니다.
이것을 다른말로 하면 양자화 정도로 표현할 수 있겠습니다. 뭔가 거창해
보이는 말이지만 연속된 값중 필요한 지점의 값들만 추려내는 과정을
의미 합니다. 역시 그림이 쉽습니다. 그림을 봅시다.
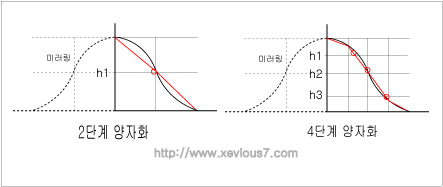
[그림] 코사인 곡선의 양자화.
그림처럼 몇등분을 하느냐에 따라서 실제 곡선은 좀더 부드러워 집니다.
기본적으로 높이맵은 격자이기 때문에 높이가 높아질수록 너비도 넓어지고
샘플링 된 값이 많아지면서 점점 더 코사인 곡선에 근접해지게 됩니다.
여기까지 전개가 되었으면 실제적으로 높이맵에 적용할 수 있는 알고리즘을 충분히
만들수 있을 것입니다.
위의 내용을 이해했다면 바로 구현을 할 수 있으리라 생각합니다.
스스로 구현해보길 추천드립니다. 그러면 더 많은 구현알고리즘이 나올수 있을
테니깐요.
아직도 모르겠다. 라는 분 과 정리를 해보면 다음과 같습니다.
높이:너비(양자화수) 가 1:1 일때 의 코사인 곡선의 적용예
가정( 높이 3.0f )
1번 3.0f
2번 1:1이므로 양자화수 3(정수)
3번 180.0f / 3.0f = 60.0f 도
4번 for( i = 1 ; i < 3 ; i++) c_value = 3.0f * ( (cos(60도)*i + 1.0f) / 2.0f );
5번 현재버덱스의 + i 버텍스에 c_value 적용
6번 현재버텍스의 - i 버텍스에 c_value 적용
7번 현재버덱스의 - dy 값에 c_value를 적용한다음 4-6번을 재귀호출한다.
위에서 높이값을 변수로 취급하면 함수가 만들어집니다.
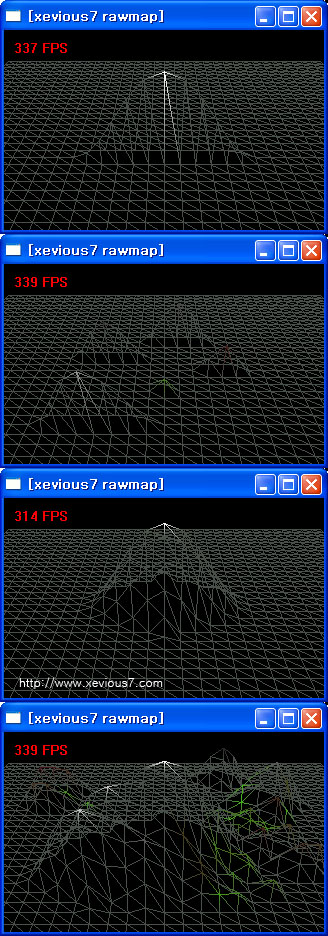
적용결과
1라인에 대한 값적용
높이에 따른 양자화의
여러예
미러링과 재귀를통한
입체화의 예
높이값조정을 통한
편집의 예
PS. 언제나 그렇듯이 제가생각한 하나의 방법이었습니다. 이런 방법도 있다는것이죠
PS. 궁금한점은 덧글을 달아주세요.
PS. 출처를 밝히고 퍼가는시는 것은 자유입니다.
PS. 제 웹페이지의 문서는 한번 포스팅으로 끝나는것이 아닌 지속적으로 보강 수정됩니다.
(링크를 걸어주세요)
추가 :! 좀더 나은 실제적 지형표현을 위한 방법.
실제 현실의세계에서의 산은 대부분 완벽 대칭적 구조를 가지지 않습니다.
위의 마지막 스샷처럼 여러개의 코사인함수 조합봉우리 모양처럼 여러개의 봉우리가
들쑥 날쭉한 비대칭구조입니다.
따라서 하나의 봉우리만 표현할때도 미러링이 아닌 좌우의 비율을 값을 조정한
비대칭인 코사인곡선 두개를 사용하여 만드는 지형생성 방법도 괜챦을 것 같습니다.
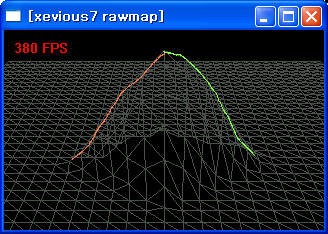
실험결과
미러링을 사용하지
않은 비대칭 코사인
곡선을 이용한
봉우리 생성의 예
(한면은 높이:양자화수가
1:1.5 이고
한면은 1:2.5) 형태
입니다.
추가 2006.8.7
참고자료 : 노이즈에 관한 자료.
랜덤으로 생성하는 자연스러운 지형생성 에 관한것은
프랙탈 기법을 이용한 지형생성( GPG1)
또는 선형보간, 펄린(Perlin) 노이즈 같은 것을 찾아보시기 바랍니다.
(펄린 노이즈는 지형생성에도 응용할 수 있지만 이펙트를 위해서 많이쓰입니다.
불이라든지 연기라든지 구름...)
http://freespace.virgin.net/hugo.elias/models/m_perlin.htm (perlin noise에 대한
자세한 설명문서)
http://gpgstudy.com/gpgiki/PerlinNoise 위문서의 해석본이 gpg에 있네요.
http://en.wikipedia.org/wiki/Perlin_noise 우리의 위키피디아 ~!!
http://www.xevious7.com/107 2006.7.21 , 최종수정 2006.8.7.
들어가는 글
3D지형에서 보통 Rawmap 이라고 불리는 높이맵 즉 높이값만 가지는
데이타를 가지고 지형을 형성할때 부드러운 모양의 지형을 만들기
위해 가장 많이 쓰여지고 있는 기법은 가우시안 함수를 이용한 기법인 것 같습니다.
확률.통계에서는 가우시안함수는 정규분포로도 잘 알려져 있으며
아주 여러분야에서 이용하고 있는 수학함수 입니다.

그런데 이 함수의 기하학적인 모양이 부드럽게 높이 솟은 산의 모양을 가지기
때문에 3D지형의 높이맵의 부드러운 지형을 위해 쓰여지는 것입니다.
물론 정밀한 손의 놀림에 의한 편집에 의해서 가능하지만 일단 어느정도
자동생성은 작업의 효율을 높이기 때문에 지형맵 툴에서 많이 사용되어지는
것 같습니다.
헌데 이 가우시안 함수는 지수함수의 공식을 가지고 있는 놈이라서
생각보다 복잡합니다. 따라서 물론 미리 계산된 셋을 가지고 적절히 조절하여
사용하는 방법을 더 많이 쓸것이고 , 아니면 소위 가우시안 필터라고 불리우는
정형화된 셋과 알고리즘을 통한 격자필터를 사용하기도 합니다. 또는 랜덤값을
통한 확률분포로 가우시안 분포를 만들어 사용하기도 합니다.
어찌 되었든 이부분에 대한 많은 문서와 구현예들이 존재하고 있습니다.
다음은 관련링크입니다.(주의: 이 링크들은 웹사이트의 사정에 의해서
깨져있을 수 있습니다.) (다른 링크를 알고 계시면 덧글을 달아주시면
감사하겠습니다. )
코사인곡선의 고찰
코사인 곡선의 모양도(사인곡선도 위상만 틀린뿐 같은 곡선이지만 계산의 편의를
위해 코사인곡선을 사용했습니다.) 완만한 산의 모양을 가지고 있습니다.
그래서 그 코사인 곡선을 이용하는 방법을 생각해보았습니다.
이 문서는 제가 생각해본 코사인 곡선을 이용한 높이맵 지형편집에 대한
문서입니다.

[그림] 코사인곡선
그림처럼 각도에 따른 값을 축으로 그린 코사인 곡선은 그림과 같은 모양을 가집니다.
여기서 우리가 필요한 부분은 0도에서 180도 부분입니다.
이 부분 값만 있으면 너비(즉 주기)를 조정해서 좀더 뽀죡해 보이는 곡선 또는
완만한 곡선이 가능하고 그것을 다시 미러링하고 회전하면 부드럽게 올라온
산또는 언덕 비슷한 모양을 만들수 있기 때문입니다.

[그림] 코사인 곡선의 고찰
코사인 곡선의 높이맵적용
아날로그적으로 이해는 쉽지만 이것을 격자로 되어있는 nxn 의 높이맵의
한 정점에 이값들을 적용시켜서 그 모양을 만들려고 생각하면 격자의 크기에 따라
값들이 일정간격별로 정해져야 합니다.
이것을 다른말로 하면 양자화 정도로 표현할 수 있겠습니다. 뭔가 거창해
보이는 말이지만 연속된 값중 필요한 지점의 값들만 추려내는 과정을
의미 합니다. 역시 그림이 쉽습니다. 그림을 봅시다.

[그림] 코사인 곡선의 양자화.
그림처럼 몇등분을 하느냐에 따라서 실제 곡선은 좀더 부드러워 집니다.
기본적으로 높이맵은 격자이기 때문에 높이가 높아질수록 너비도 넓어지고
샘플링 된 값이 많아지면서 점점 더 코사인 곡선에 근접해지게 됩니다.
여기까지 전개가 되었으면 실제적으로 높이맵에 적용할 수 있는 알고리즘을 충분히
만들수 있을 것입니다.
위의 내용을 이해했다면 바로 구현을 할 수 있으리라 생각합니다.
스스로 구현해보길 추천드립니다. 그러면 더 많은 구현알고리즘이 나올수 있을
테니깐요.
아직도 모르겠다. 라는 분 과 정리를 해보면 다음과 같습니다.
코사인함수곡선의 높이맵 적용 알고리즘
1. 코사인함수 곡선의 정점(0도)에 해당하는 높이값을 정한다.
2. 높이값에 따라서 너비를 구하고 양자화할 수를 계산한다.
3. 180 / 양자화수를 하여 구해야될 코사인함수값의 각도들을 정한다.
4. 원래 정한 높이에 정규화한 코사인함수값( (값+1.0f) / 2.0f ) 을 곱하여
각각 각도에서의 실제 높이값을 구한다
( 정규화된 코사인값은 원래높이에 대한 비율이된다.)
5. 정점에 적용한다.
6. 미러링을 한다.
7. 양자화수 만큼 다음곡선에 적용하여 입체를 생성한다.
1. 코사인함수 곡선의 정점(0도)에 해당하는 높이값을 정한다.
2. 높이값에 따라서 너비를 구하고 양자화할 수를 계산한다.
3. 180 / 양자화수를 하여 구해야될 코사인함수값의 각도들을 정한다.
4. 원래 정한 높이에 정규화한 코사인함수값( (값+1.0f) / 2.0f ) 을 곱하여
각각 각도에서의 실제 높이값을 구한다
( 정규화된 코사인값은 원래높이에 대한 비율이된다.)
5. 정점에 적용한다.
6. 미러링을 한다.
7. 양자화수 만큼 다음곡선에 적용하여 입체를 생성한다.
높이:너비(양자화수) 가 1:1 일때 의 코사인 곡선의 적용예
가정( 높이 3.0f )
1번 3.0f
2번 1:1이므로 양자화수 3(정수)
3번 180.0f / 3.0f = 60.0f 도
4번 for( i = 1 ; i < 3 ; i++) c_value = 3.0f * ( (cos(60도)*i + 1.0f) / 2.0f );
5번 현재버덱스의 + i 버텍스에 c_value 적용
6번 현재버텍스의 - i 버텍스에 c_value 적용
7번 현재버덱스의 - dy 값에 c_value를 적용한다음 4-6번을 재귀호출한다.
위에서 높이값을 변수로 취급하면 함수가 만들어집니다.

적용결과
1라인에 대한 값적용
높이에 따른 양자화의
여러예
미러링과 재귀를통한
입체화의 예
높이값조정을 통한
편집의 예
PS. 언제나 그렇듯이 제가생각한 하나의 방법이었습니다. 이런 방법도 있다는것이죠
PS. 궁금한점은 덧글을 달아주세요.
PS. 출처를 밝히고 퍼가는시는 것은 자유입니다.
PS. 제 웹페이지의 문서는 한번 포스팅으로 끝나는것이 아닌 지속적으로 보강 수정됩니다.
(링크를 걸어주세요)
추가 :! 좀더 나은 실제적 지형표현을 위한 방법.
실제 현실의세계에서의 산은 대부분 완벽 대칭적 구조를 가지지 않습니다.
위의 마지막 스샷처럼 여러개의 코사인함수 조합봉우리 모양처럼 여러개의 봉우리가
들쑥 날쭉한 비대칭구조입니다.
따라서 하나의 봉우리만 표현할때도 미러링이 아닌 좌우의 비율을 값을 조정한
비대칭인 코사인곡선 두개를 사용하여 만드는 지형생성 방법도 괜챦을 것 같습니다.

실험결과
미러링을 사용하지
않은 비대칭 코사인
곡선을 이용한
봉우리 생성의 예
(한면은 높이:양자화수가
1:1.5 이고
한면은 1:2.5) 형태
입니다.
추가 2006.8.7
참고자료 : 노이즈에 관한 자료.
랜덤으로 생성하는 자연스러운 지형생성 에 관한것은
프랙탈 기법을 이용한 지형생성( GPG1)
또는 선형보간, 펄린(Perlin) 노이즈 같은 것을 찾아보시기 바랍니다.
(펄린 노이즈는 지형생성에도 응용할 수 있지만 이펙트를 위해서 많이쓰입니다.
불이라든지 연기라든지 구름...)
http://freespace.virgin.net/hugo.elias/models/m_perlin.htm (perlin noise에 대한
자세한 설명문서)
http://gpgstudy.com/gpgiki/PerlinNoise 위문서의 해석본이 gpg에 있네요.
http://en.wikipedia.org/wiki/Perlin_noise 우리의 위키피디아 ~!!